21. Multiple Integrals in Curvilinear Coordinates

b. Integrating in Cylindrical Coordinates

4. Converting & Mixing, Rectangular & Cylindrical Coordinates

Sometimes it is useful to use cylindrical coordinates instead of rectangular coordinates when computing an integral. Other times it is best to use rectangular coordinates for one part of an integral and cylindrical coordinates for another part.

Converting Rectangular to Cylindrical Coordinates

Sometimes the antiderivative of the integrand is not known, making the integral difficult, if not impossible. By converting to cylindrical coordinates, we may be able to simplify the integral greatly.

Compute the integral \(\displaystyle I =\int_0^{3/\sqrt{2}}\int_y^{\sqrt{9-y^2}}\int_0^{x^2+y^2} \cos(z)\,dz\,dx\,dy\)

This integral is very hard to do in rectangular coordinates. The \(z\)-integral can be easily done, but then the \(x\)-integral is impossible since we do not know the \(x\)-antiderivative of \(\sin(x^2+y^2)\). However, converting to cylindrical coordinates drastically simplifies the problem.

First, we plot the base region in the \(xy\) plane. From the integral, we see that the region of integration is \(y \le x \le \sqrt{9-y^2}\) which is shaded in blue. The left and right curves intersect when \[ y=\sqrt{9-y^2} \quad \Rightarrow \quad 2y^2=9 \quad \Rightarrow \quad y=\pm\dfrac{3}{\sqrt{2}} \] The upper limit for \(y\) is \(\dfrac{3}{\sqrt{2}}\) which is precisely the intersection point and the lower limit is \(y=0\) as shown in the plot.

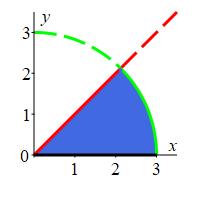
The plot shows the 8th of a circle of radius 3 between the x axis and the line y = x.

We now convert to cylindrical coordinates. We replace the volume differential by: \[ dV=dz\,dx\,dy=r\,dz\,dr\,d\theta \] and the new limits are: \[ 0 \le \theta \le \dfrac{\pi}{4} \qquad 0 \le r \le 3 \quad \text{and} \quad 0 \le z \le r^2 \] So the integral becomes \[\begin{aligned} I&=\int_0^{\pi/4}\int_0^{3}\int_0^{r^2} \cos(z)\,r\,dz\,dr\,d\theta =\dfrac{\pi}{4}\int_0^{3} \left[\sin(z)\dfrac{}{}\right]_0^{r^2}\,r\,dr \\ &=\dfrac{\pi}{4}\int_0^{3} \sin(r^2)\,r\,dr =\dfrac{\pi}{4}\left[-\,\dfrac{1}{2}\,\cos(r^2)\right]_0^3 \\ &=\dfrac{\pi}{8}(-\cos(9)+\cos(0)) =\dfrac{\pi}{8}(1-\cos(9)) \end{aligned}\]

Compute the integral \(\displaystyle I=\int_{-2\sqrt2}^{2\sqrt2}\int_{|x|}^{\sqrt{16-x^2}} \int_0^{x^2+y^2} e^{-z}\,dz\,dy\,dx\)

Start by looking at the limits on the \(y\) integral.

\(I = \dfrac{\pi}{4}(15+ e^{-16}) \approx 11.781\)

The limits on the \(y\) integral tell us the region is between \(|x|\) and the circle of radius \(4\) as shown in the plot. To find where they intersect we equate the \(2\) curves: \[\begin{aligned} |x| = \sqrt{16-x^2} \quad \Rightarrow \quad 2x^2 = 16 \quad \Rightarrow \quad x = \pm 2\sqrt{2} \end{aligned}\] The limits for \(x\) are \(2\sqrt{2}\) and \(-2\sqrt{2}\), which are precisely the intersection points shown in the plot.

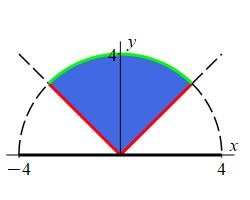
The plot shows the circle of radius 4 centered at the origin and the sector above the two 45 degree lines.

We now convert to cylindrical coordinates. We replace the volume differential by: \[ dV=dz\,dy\,dx=r\,dz\,dr\,d\theta \] and the new limits are: \[ \dfrac{\pi}{4} \le \theta \le \dfrac{3\pi}{4} \qquad 0 \le r \le 4 \quad \text{and} \quad 0 \le z \le r^2 \] So the integral becomes \[\begin{aligned} I &=\int_{\pi/4}^{3\pi/4}\int_0^4 \int_0^{r^2} e^{-z}\,r\,dz\,dr\,d\theta = \dfrac{\pi}{2} \int_0^4 \left[\rule{0pt}{10pt}-e^{-z}\right]_0^{r^2}\,r\,dr \\ &= \dfrac{\pi}{2} \int_0^4 r-re^{-r^2}\,dr = \dfrac{\pi}{2} \left[\dfrac{1}{2}r^2+\dfrac{1}{2}e^{-r^2}\right]_0^4 \\ &= \dfrac{\pi}{2}(8 + \dfrac{1}{2}e^{-16} - \dfrac{1}{2}) = \dfrac{\pi}{4}(15+ e^{-16}) \approx 11.781 \end{aligned}\]

mj,ad 

Mixing Rectangular and Cylindrical Coordinates

Sometimes one integral should be done in rectangular coordinates and another should be done in cylindrical coordinates, such as in the example below.

The cube \(-3 \le x \le 3\) and \(-3 \le y \le 3\) and \(0 \le z \le 6\) is cut out of the cone \(0 \le z \le 12-r\). Find the mass of the remaining part of the cone if the mass density is \(\delta=x^2+y^2=r^2\).

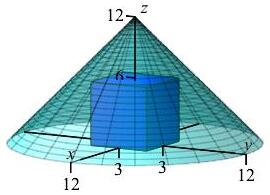
The plot showe a cube inside a cone with its vertex at the top.

We compute the mass of the cone including the cube and then subtract the mass of the cube.

Using cylindrical coordinates, the mass of the cone including the cube is: \[\begin{aligned} M_\text{cone} &=\iiint\limits_\text{cone} \delta \,dV =\int_0^{2\pi}\int_0^{12}\int_0^{12-r} r^2\cdot r\,dz\,dr\,d\theta \\ &=2\pi\int_0^{12} r^3\left[z\dfrac{}{}\right]_{z=0}^{12-r}\,dr =2\pi\int_0^{12} r^3(12-r)\,dr \\ &=2\pi\left[3r^4-\dfrac{r^5}{5}\right]_0^{12} =2\pi\left(3\cdot12^4-\dfrac{12^5}{5}\right) \\ &=2\pi12^4\left(3-\dfrac{12}{5}\right) =\dfrac{6\cdot12^4\pi}{5} \end{aligned}\] Using rectangular coordinates, the mass of the cube is: \[\begin{aligned} M_\text{cube} &=\iiint\limits_\text{cube} \delta \,dV =\int_0^6\int_{-3}^3\int_{-3}^3 (x^2+y^2)\,dx\,dy\,dz \\ &=\int_0^6 \,dz \left(\int_{-3}^3 x^2\,dx\int_{-3}^3 \,dy +\int_{-3}^3 \,dx\int_{-3}^3 y^2\,dy\right) \\ &=\left[\rule{0pt}{10pt}z\right]_0^6 \left(\left[\dfrac{x^3}{3}\right]_{x=-3}^3\left[y\dfrac{}{}\right]_{y=-3}^3 +\left[x\dfrac{}{}\right]_{-3}^3\left[\dfrac{y^3}{3}\right]_{-3}^3\right) \\ &=6(18\cdot6+6\cdot18)=1296 \end{aligned}\] Thus, the mass inside the cone but outside the cube is \[ V=\dfrac{6\cdot12^4\pi}{5}-1296\approx76877. \]

A cylinder of radius \(2\) is drilled through a \(6 \times 6 \times 4\) rectangular solid as shown in the plot. Find the average value of the square of the distance from the \(z\)-axis \(f(x,y)=x^2+y^2=r^2\) on the remaining solid.
Recall: The average value of a function \(f\) on a region is \[ f_\text{ave}=\dfrac{1}{V}\iiint f\,dV \]

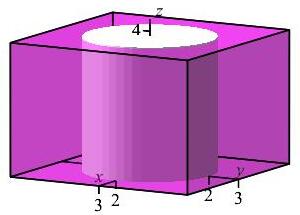
The plot shows a box with sides -3 < x < 3, -3 < y < 3 and 0 < z < 4. A cylinder of radius 2 has been removed along the z axis.

Find the volume of the box and the cylinder and subtract.
Find the integral of \(f\) on the box and the cylinder and subtract.

\(f_{\text{ave}} = \dfrac{54-2\pi}{9-\pi} \approx 8.145\)

We compute the integral of the function over the rectangular solid and subtract the integral of the function over the cylinder, then divide the result by the volume of the remaining solid.

Using rectangular coordinates, the integral of the function over the entire rectangular solid is: \[\begin{aligned} \iiint\limits_\text{rectangle} f \,dV &=\int_0^4\int_{-3}^3\int_{-3}^3 (x^2+y^2)\,dx\,dy\,dz \\ &=\int_0^4 \,dz \left(\int_{-3}^3 x^2\,dx\int_{-3}^3 \,dy +\int_{-3}^3 \,dx\int_{-3}^3 y^2\,dy\right) \\ &=\left[\rule{0pt}{10pt}z\right]_0^4 \left(\left[\dfrac{x^3}{3}\right]_{x=-3}^{x=3}\left[\rule{0pt}{10pt}y\right]_{y=-3}^{y=3} +\left[\rule{0pt}{10pt}x\right]_{x=-3}^{x=3}\left[\dfrac{y^3}{3}\right]_{y=-3}^{y=3}\right) \\ &=4(18\cdot6+6\cdot18)=864 \end{aligned}\] Using cylindrical coordinates, the integral of the function over the cylinder is: \[\begin{aligned} \iiint\limits_\text{cylinder} f\,dV &=\int_0^{2\pi}\int_0^{2}\int_0^{4} r^2\cdot r\,dz\,dr\,d\theta \\ &=2\pi\int_0^{2} r^3\left[\rule{0pt}{10pt}z\right]_{z=0}^{z=4}\,dr =8\pi\int_0^{2} r^3\,dr \\ &=8\pi\left[\dfrac{1}{4}r^4\right]_0^{2} =32\pi \end{aligned}\] Thus the integral of the function over the remaining solid is: \[\begin{aligned} \iiint\limits_\text{solid} f\,dV = \iiint\limits_\text{rectangle} f\,dV - \iiint\limits_\text{cylinder} f\,dV = 864 - 32\pi \end{aligned}\] We can easily find that the volume of the remaining solid is: \[\begin{aligned} V_{\text{solid}} = V_{\text{rectangle}} - V_{\text{cylinder}} = 6\cdot6\cdot4 - \pi\cdot2^2\cdot4 = 144-16\pi \end{aligned}\] Finally we can compute \[ f_{\text{ave}} = \dfrac{1}{V_{\text{solid}}}\iiint\limits_\text{solid} f\,dV = \dfrac{864-32\pi}{144-16\pi} = \dfrac{54-2\pi}{9-\pi} \approx 8.145 \]

mj,ad 

© MYMathApps

Supported in part by NSF Grant #1123255